Markov Decision Processes
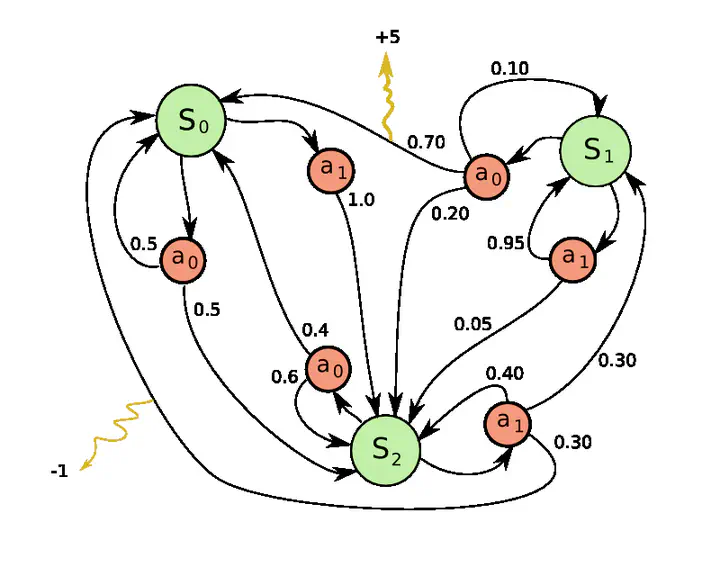 An example of a MDP with 3 states and 2 applicable actions per state
An example of a MDP with 3 states and 2 applicable actions per stateAutomated planning is a branch of Artificial Intelligence (AI) aiming at finding optimal plans to achieve goals. Planning problems with non-deterministic actions are known to be much harder to solve. Markov Decision Processes (MDPs) are generally used to solve such planning problems that can be represented using a probabilistic model of applicable actions. Some classical algorithms such as Value Iteration (VI) and Policy Iteration (PI) can be used to find an optimal policy of an MDP. Unfortunately, due to the curse of dimensionality, most MDP planning domains have too many states to be able to be solved in a reasonable time using these algorithms.
Several state-of-the-art MDP algorithms have been proposed to increase the speed of computation. Many of them are able to focus on the most promising parts of the MDP through heuristic search algorithms such as LRTDP or LAO*. Some other MDP algorithms use partitioning methods to decompose the state-space in smaller parts. For example, the P3VI (Partitioned, Prioritized, Parallel Value Iteration) and the TVI (Topological Value Iteration) algorithms decompose the state-space and then solve each part separately.
An orthogonal way to improve computation speed is to consider how these algorithms are actually implemented. In this project, we propose to take account of low-level elements such as the memory hierarchy and the different levels of parallelism of modern computers in the context of MDP planning algorithms. We propose a new memory representation of MDP, which we call CSR-MDP, that aims at improving the cache memory access patterns (for whatever planning algorithm that is used). We also propose a parallel version of the TVI algorithm, pcTVI (for parallel-chained TVI).
In this project, we developed an SSP-MDP planning C++ Library that supports classical algorithms (e.g., VI, LRTDP, TVI, etc.) as well as our proposed new planning algorithms (pcTVI, eTVI, eiTVI) with our new MDP memory representation, CSR-MDP.